When it comes to algorithms you will often hear very polarizing sentiments amongst developers. While some cringe at the thought of the overwhelming complexity associated with them, others yearn for the challenges that they pose, knowing just how valuable they truly are. Nonetheless algorithms are undoubtably one of the most powerful concepts in computer science. By generating a strategic list of executable steps, called a function, programmers can instruct computers to execute large, complex algorithms at scale. Given the limitations of the human brain, this disparity is ultimately what solidifies the true power of computation. If algorithms themselves don't overwhelm you enough, just a friendly reminder that there are millions, if not billions (if not an infinite number) of different algorithms. Truly mind blowing! In computer programming however, algorithms can typically be broken down and classified into just a handful of different types. In this writing we are going to look at one of the most common search algorithms, the Binary Search.

What Is Binary Search?

Binary Search (also known as Half-Interval Search, Logarithmic Search, or Binary Chop) is an algorithm that finds the position of a target value within a sorted array by continuously halving the array upon each search iteration. The algorithm compares the target value to the middle element of the array. If the two values are not equal, the half in which the target cannot lie is eliminated and the search continues iterating over the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the remaining half proves empty upon the conclusion of the search, the array does not contain the target.

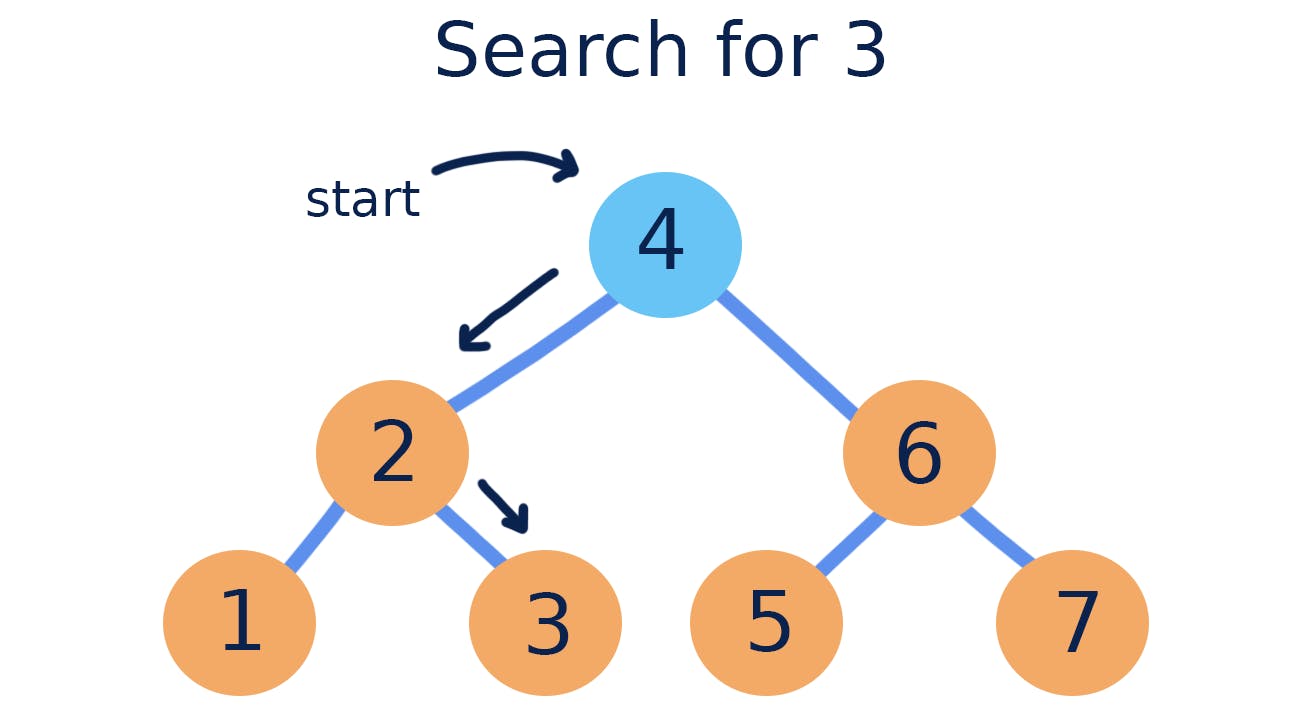
"Big O" Notation Considerations

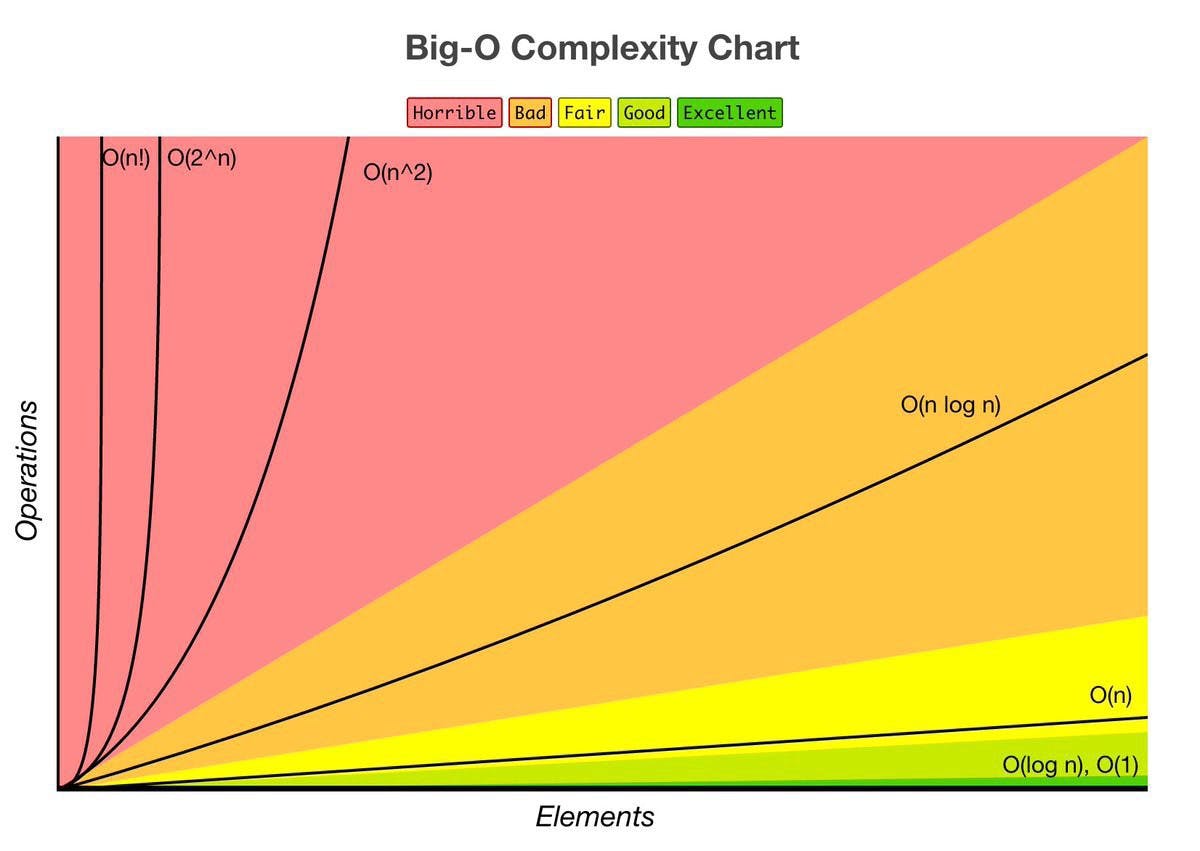
The "Big O" Notation in the realm of computer science, is essentially just nerdy math jargon for how efficient an algorithm is, as it relates to the run time and space requirements necessary to complete it. It ultimately serves as a way to categorize and quantify the performance of a given algorithm based on it's run. Depending on this complexity, algorithms are categorized into a handful of different math classes. In worst case scenario Binary Search runs in logarithmic time, making O(log n), where n is the number of elements in the array. In best case scenario it runs constant 0(1).

Efficiencies and Limitations of Binary Search

Efficiencies

Depending on the quantity of data, Binary Search is typically a much faster approach than a Linear Search for instance. Linear Search compares data in sequential order, from the starting index until the function has either been satisfied, or the end of the array. This differs from Binary Search in that every element of proceeding data must be iterated through before moving on, which can ultimately prove to be a major limitation, especially when dealing with large datasets. Using the halving technique, Binary Search can move through the data much more efficiently considering it doesn't necessarily need to touch every element in order, since it will follow the path of least resistance. Imagine the target value was at the end of a large array. Linear Search could take you a near lifetime!

Limitations

One consideration however is that in order for a Binary Search to shine in this fashion, the data must first be sorted properly to ensure the efficiency of the iterations. So while it can be an extremely efficient solution in most environments, it doesn't necessarily come that way "out of the box". Given the non-linear trek that a Binary Search makes, deficiencies can also arise in small datasets where the excessiveness of Binary Search is just plain overkill.

The Code

So how does Binary Search really operate under the hood?

Here's the anatomy:

function binarySearch(arr, val) {
  let start = 0;
  let end = arr.length - 1;

  while (start <= end) {
    let mid = Math.floor((start + end) / 2);

    if (arr[mid] === val) {
      return mid;
    }

    if (val < arr[mid]) {
      end = mid - 1;
    } else {
      start = mid + 1;
    }
  }
  return -1;
}

let arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
console.log(binarySearch(arr, 8))
// 7 
// (value 8 is in the 7th index of the zero-indexed array)

Conclusion

While it isn't perfect, there's no doubt that Binary Search is one of the more efficient and speedy routes to consider taking when searching for an element within a list of pre-sorted data. By continuously halving the array, Binary Search takes a path of minimal resistance and can accomplish the same outcome of other algorithms, often in much fewer steps. It's definitely a wise idea to keep Binary Search in your back-pocket, even more so as your data continues to scale!